Abstract
The dynamic range of optical fiber refractive index sensors is mainly determined by the refractive index (RI) of the sensor surface in contact with the sample under test. In case of the refractive index sensor based on the hybrid fiber Fabry–Perot interferometer (HFFPI), the largest measurable refractive index value is equal to that of the fiber core. In this work, we demonstrate that it is possible to extend the refractive index dynamic range of a HFFPI by simply adjusting the optical path length (OPL) of the air and solid cavity to be equal or differ by just a small amount. Two isometric versions of the HFFPI (i-HFFPI) with a total length of 100 and 172 μm, where the OPL of the air and solid cavity are very similar, were fabricated and tested. The interferometers were immersed in different samples with a refractive index ranging from 1.000 to 1.733. The response of the interferometers was analyzed in the Fourier domain, and it was possible to establish a one-to-one relationship between the refractive index of the liquid sample and the amplitude of one of the peaks in the Fourier spectra. The amplitude of this peak experienced a linear increment when the RI of the surrounding medium was increased. Tracking the amplitude changes of a Fourier spectrum peak is straightforward which simplifies the online monitoring of the sensor. These features make this compact refractive index fiber sensor very appealing for biosensing applications.
Introduction
Fresnel reflection-based optical fiber refractive index sensors (FR-OFRIS) have proliferated in recent years since their structure is very simple, but also because the sensor interrogation is through monitoring the change in the intensity of the light reflected at the fiber tip end-face (Ran et al., 2008; Gong et al., 2010a; Gong et al., 2010b; Choi et al., 2010; Wang and Wang, 2012; Jiang et al., 2013b; Jáuregui-Vázquez et al., 2013; Chen et al., 2017; Zhu and Huang, 2021). The first and yet simplest approach was reported in 1987, and it basically consisted of a single-mode fiber tip, a laser, a beam splitter, and photodetectors (Meyer and Eesley, 1987). Since then, an important number of fiber-optic sensors to detect physical, chemical, or biological magnitudes using FR-OFRIS have been proposed. Because of their unique features, it is expected that these devices could evolve and, eventually, replace the current refractive index monitoring techniques used in clinical diagnosis (Li, 2020), in petrochemical industries (Joel and Okoro, 2019), or in food and beverage production (Aronne and Malara, 2019), since it is well known that these devices take advantages of the inherent characteristics of optical fiber technology. In some cases, optical fiber sensors are the most suitable or even the unique technological solution, for example, when the amount of the sample or the access to the sample location is a concern. In order to fulfill the demanding requirements of some applications, three important issues, regarding the performance of the FR-OFRIS, must be addressed: first, the relatively poor resolution of these devices compared with that displayed by the evanescent wave-based optical fiber sensors; second, it is well known that the FR-OFRIS response is basically dependent on the changes of the intensity reflected by the fiber tip end-face, and then the accuracy and repeatability of these devices are determined by the optical source stability; and finally, these devices exhibit refractive index ambiguity, that is, two samples with a different refractive index could produce the same intensity response. Ambiguity has a negative impact since it limits the refractive index measurement dynamic range of the FR-OFRIS. Different strategies have been followed to enhance the sensitivity and resolution or increase the dynamic range of these fiber refractometers, but the most successful one involved the exploitation of the optical interference phenomenon. Interesting FR-OFRIS based on multimode interference (MI) (Brientin et al., 2021), strong coupled multicore fiber interferometers (SCMCFI) (Flores-Bravo et al., 2021), Michelson interferometers (MiI) (Meng et al., 2011), or hybrid fiber Fabry–Perot interferometers (HFFPI) (Wang and Wang, 2012; Jiang et al., 2013a; Jiang et al., 2013b; Liu et al., 2017; Rodríguez-Quiroz et al., 2019; Zhang et al., 2021) have been demonstrated. Although the different versions of the interferometric FR-OFRIS proposed so far have contributed to improving the sensitivity and resolution, only the HFFPI version of the FR-OFRIS demonstrated that it is possible to avoid the refractive index ambiguity (Dominguez-Flores et al., 2020a; Rodríguez-Quiroz et al., 2020). To avoid the refractive index ambiguity, it was necessary to deposit a high refractive index thin film in the end-face of the fiber tip (Jiang et al., 2013a; Dominguez-Flores et al., 2020b), to make a post-processing analysis of the reflectance (Dominguez-Flores et al., 2020a), or to photo-imprint an optical fiber Bragg grating in series with the HFFPI (Rodríguez-Quiroz et al., 2020).
In this work, we demonstrate that it is possible to increase the dynamic range of a refractive index-based HFFPI sensor by adjusting the OPL of the air and solid cavity. Typically, the largest refractive index value that can be measured with a HFFPI is smaller than that of the effective RI of the fundamental mode of the SMF core. Two isometric HFFPI (i-HFFPI), with a total physical length of 100 and 172 μm, were fabricated and tested to demonstrate that it is possible to measure the refractive index of the fiber surrounding the medium in a range from 1.000 to 1.733, without ambiguity. This is the first time, to our knowledge, that such ultra-long refractive index dynamic is measured directly from the reflectance of the HFFPI that consists of a capillary fiber (CF) in series with a segment of the single-mode fiber (SMF). The response of the interferometers was analyzed in the Fourier domain; the reflectance exhibited a series of peaks whose amplitude was modulated by the refractive index of the external medium. It was possible to establish a one-to-one relationship between the amplitude of one of the peaks of the Fourier spectrum and the refractive index of the surrounding media. To our knowledge, the largest refractive index dynamic range was measured without ambiguity using fiber-optic sensors (Zhou et al., 2011; Lu et al., 2012; Jáuregui-Vázquez et al., 2013; Liu et al., 2013; Li et al., 2014; Urrutia et al., 2019).
Principle of Operation of the Sensor and Fabrication Process
Analysis of the Characteristic Reflectance of the i-HFFPI
The process to fabricate the HFFPIs analyzed in this work can be described as follows: first, a CF was spliced to a SMF, and then the CF was cleaved to leave a section of length . After that, a SMF was spliced to the free end of the CF. Finally, the SMF was cleaved to obtain an SMF section of length . The final structure of a HFFPI is represented in Figure 1. The OPL is defined by the product of the physical length and refractive index of the path material; therefore, the OPL of air and solid cavity of the HFFPI are defined by and , respectively. In this case, and represent the refractive index of air and glass of the SMF core, respectively. An i-HFFPI is obtained when the is equal or very similar to the . It is well known that the mathematical expression of the reflectance of a HFFPI contains three interference terms produced by the superposition of the three beams reflected by the three interfaces of the air and solid cavities, and can be described by the following equation (Rodríguez-Quiroz et al., 2019):where is the wavelength of the light, represents the reflectance of the first and second interface of the air cavity, respectively, and the reflectance of the third interface between a SMF and the external medium is . denote the phase induced in the reflected beam at the first, second, and third interface, respectively, and , where and represent the loss factors in cavities. The reflectance spectrum of an i-HFFPI, that is, when is simpler, and the first two interference terms of Eq. 1 are almost equal, and so this equation can be reduced into two interference terms, and the cosine argument of the first term is twice that of the second. Commonly, the analysis of the refractometric response of a HFFPI is carried out in the optical domain (Zhang et al., 2018). The characteristic spectra of a HFFPI in the Fourier domain are shown in Figure 2A. These graphs were obtained by simulating the response of a HFFPI using Eq. 1 and then calculating the Fourier transform using the algorithm described by Rodríguez-Quiroz et al. (2019). In these simulations, the OPL of the air cavity was kept constant and equal to 94.23 µm while the solid cavity OPL was varied. When is significantly larger than , the Fourier spectrum exhibits three peaks as can be seen in the black line graph of Figure 2A; this HFFPI configuration has been extensively studied. In order to identify each peak, they were labeled as , , and , the position of each one indicates the optical path length of the air, solid, and solid plus air cavity, respectively. The spectra were normalized to the maximum amplitude of when the maximum amplitude of occurs at 50.74 µm; thus, it is possible to declare that 50.74 µm. When the solid cavity length is increased, shifts toward larger OPL values and eventually when is slightly shorter than , only two peaks labeled as and appears as can be seen in the orange spectrum of Figure 2A. The amplitude of the peak , resulting from the overlapping of and , is smaller than the amplitude of the original . When was exactly equal to , the overlapping peak reached its largest amplitude (pink spectrum). Then the amplitude decreases when the is slightly larger than the (dark green spectrum). The position of peak P3 exhibits a red shift when is increased, but its amplitude remains constant. In this simulation, 1.000 and 1.449.
FIGURE 1
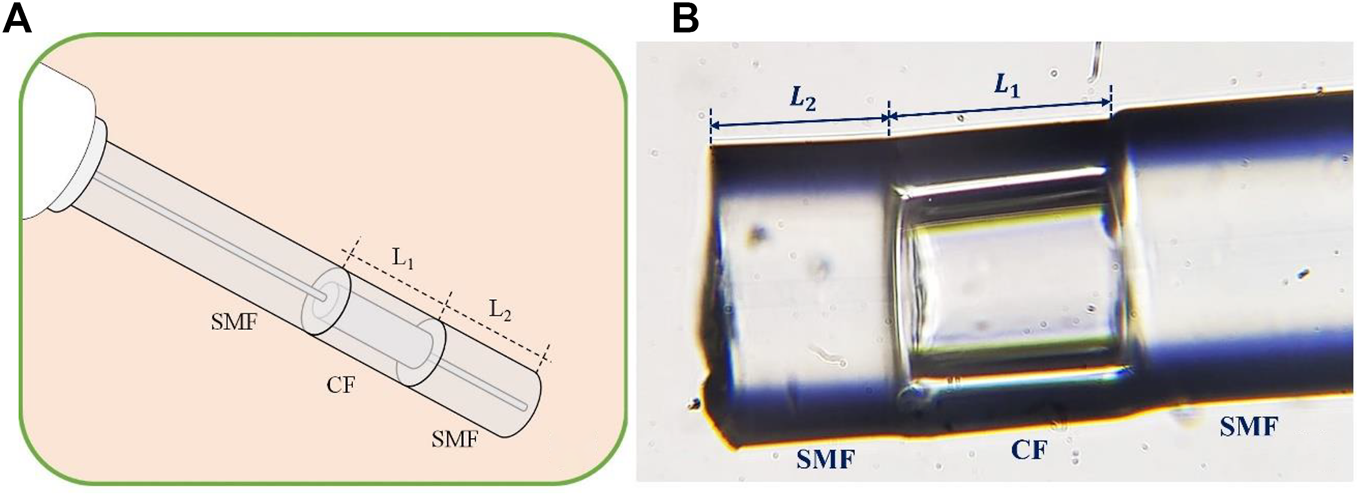
(A) Schematic representation and (B) microscope image of an i-HFFPI.
FIGURE 2
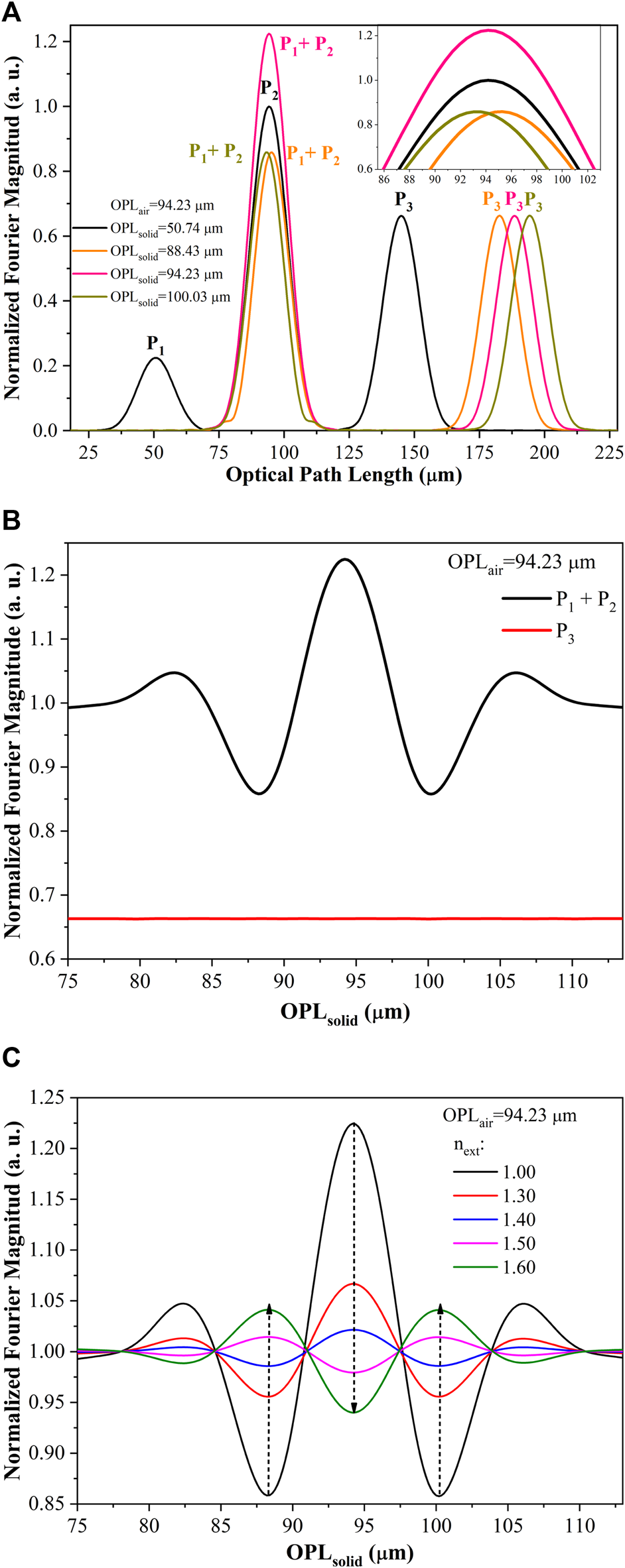
(A) Reflectance of the HFFPI in the Fourier domain and (B) maximum amplitude of the overlapped (black line) and (red line) peaks to different while the was constant. (C) Changes in the maximum amplitude of the overlapped peak for different values of the external refractive index (next). The direction of the arrows indicates a decrement or an augment of the amplitude.
In order to elucidate the behavior of the amplitude of the resulting peak , a simulation study was carried out. The optical path length of the air cavity was fixed, 94.23 µm. The optical path length of the solid cavity , that is, the length of the SMF, was varied from an initial value of 75 µm, and was increased with steps of 0.1 µm until a final value of 115 µm was reached. Then the optical reflection spectrum was calculated using Eq. 1, and finally, these spectra were transformed to the Fourier domain. The amplitude of the peak for each value of the is shown in Figure 2B. Depending on the overlapping of the peaks and , corresponding to the solid and air cavity, respectively, the amplitude of the peak drops 15% or increases by ∼23% compared with the amplitude of the . This overlapping condition can be accomplished experimentally, according to the results of the simulation presented in Figure 2B, when the length difference between the CF and an SMF is smaller than 9 µm.
The effect of the RI of the external medium in the amplitude of the peak was also studied. In Figure 2C, the simulated amplitude of the i-HFFPI was shown when was equal to 1.00, 1.30, 1.40, 1.50, and 1.60. It can be seen that when the OPL of air and solid cavities are equal, the increment of produces a decrement in the amplitude of the peak. In contrast, when the is larger or smaller than the by 5.8 µm, the amplitude of the peak increases when the increases. The most remarkable aspect in the response of the i-HFFPI, according to the simulation, is the absence of ambiguity; that is, each value of can be associated with one and only one peak amplitude. This response is due to the changes in the amplitude of peak since it is well known that the amplitude of is not affected by the changes in the external medium refractive index.
Experimental Refractometric Response of i-HFFPI
From the aforementioned discussion, several i-HFFPI were fabricated by splicing a single-mode fiber (SMF-28) and a capillary fiber (CF, ID 56/OD 125) using a commercial fiber splicer (Fitel s178) and a fiber cleaver. A SMF was spliced to the CF to form the air-cavity of length , then the CF was cleaved and spliced to another SMF, and finally, the SMF was cleaved leaving a section of length . During each stage of the fabrication process, the reflectance of the device was monitored, and some spectra were recorded using the optical sensor interrogator (Hyperion si255 from Micron Optics). The optical reflectance of an i-HFFPI with cavity lengths of and is shown in Figure 3A, and the black line spectrum was obtained when the fiber tip was surrounded by air. The i-HFFPI tip was immersed in several liquid samples; the procedure can be described as follows: first, the fiber tip was cleaned by immersing it in water; after a minute, the fiber was taken off and dried with compressed air; and then it was immersed in ethanol for another minute and dried with air. The procedure was repeated another two times, and finally, the fiber was immersed in the sample for 5 min. Before and after immersing the fiber in the liquid samples under test, it was cleaned following the procedure described. In Figure 3A, it is possible to see the optical spectra obtained when the fiber tip was immersed in the liquid samples. The amplitude of the peaks in the spectra increases as the value of increases but as was expected, no spectrum shift was observed. The Fourier transforms of these spectra are shown in Figure 3B. Only two peaks are observed, and all the spectra were normalized to the maximum amplitude of the first peak when the fiber was surrounded by air. Since the is around 3.4 µm larger than , when the fiber tip was immersed into the liquids, the amplitude of the first peak exhibited an increment. On the other hand, the amplitude of the second peak decreased when the fiber tip was immersed in liquids with refractive indexes of 1.318, 1.387, and 1.446. When the fiber was immersed in the last liquid, the amplitude of the peak reached a minimum, but when liquids with a larger refractive index than 1.446 were used, the peak amplitude increased. The changes in the amplitude of the first and second peaks of the Fourier spectra obtained when the fiber tip was immersed in different liquids are shown in Figure 3C. The first peak showed an increment of the amplitude as the external refractive index was increased. No ambiguity was observed in the behavior of the amplitude of the first peak; thus, it was possible to construct a characterization curve (black balls) that was approximated by a straight line (dotted black line) with a positive slope of 0.60 RIU−1. In contrast, the amplitude of the second peak decreased for a refractive index smaller than 1.4459 and increased for higher values (red balls), and this is the characteristic ambiguous behavior of a HFFPI.
FIGURE 3
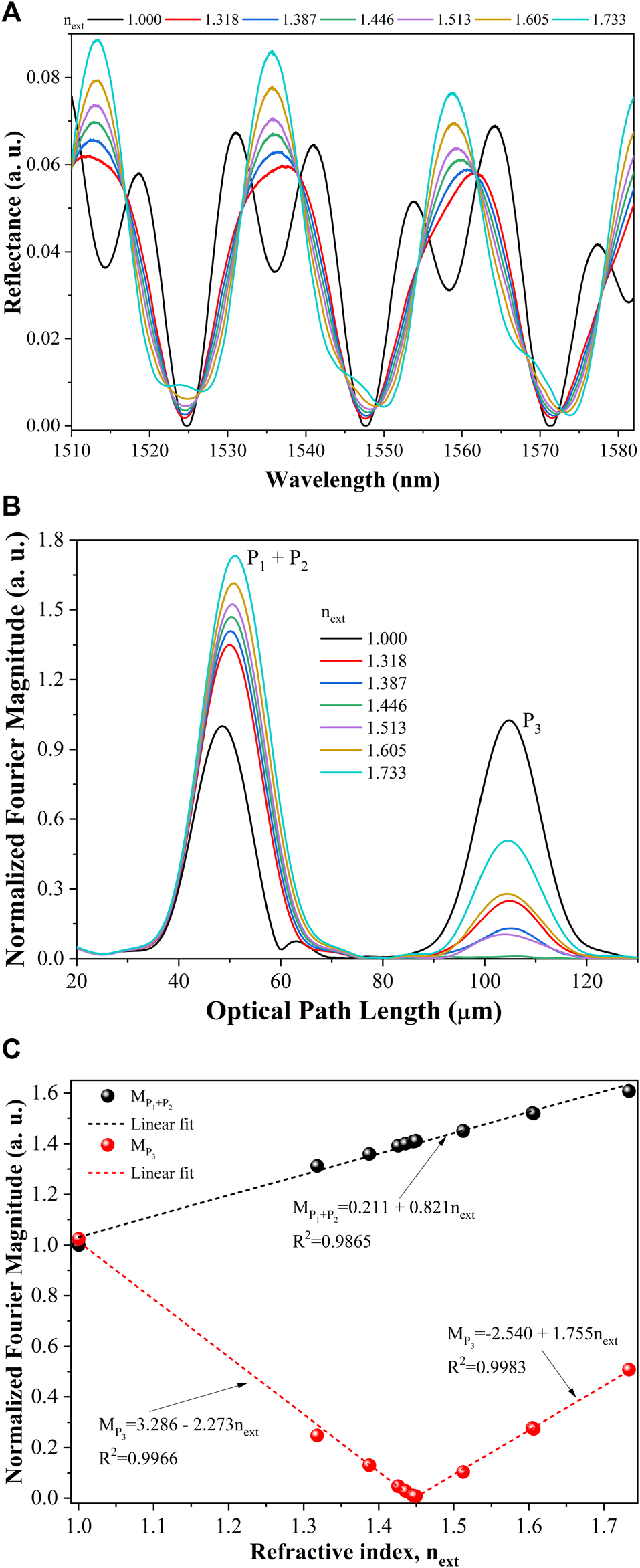
(A) Experimental spectra of the optical reflectance and (B) the corresponding Fourier transform. (C) Changes in the magnitude of the Fourier spectra peak when the i-HFFPI was immersed in different Cargille oils.
One important aspect of the response of these devices is the analysis of the stability in time and the analysis of the repeatability. The i-HFFPI with cavity lengths of and was immersed in Cargile oil with the highest refractive index of our series, with cavity lengths of . The refractometric response of the device proposed here is highly dependent on temperature. We have observed that temperature increments produce an augment in the length of the SMF section, producing a change in the amplitude of the overlapping peak. Therefore, the refractive index measurement must be done at a fixed temperature. We used a Mini Dry Bath to maintain the temperature of the samples fixed. Prior the refractive index measurements, an Eppendorf was filled with the sample under test, then the container was put inside one of the receptacles of the Dry Bath and the temperature was fixed. Then the i-HFFPI was carefully immersed in the liquid sample, avoiding touching the bottom and the walls of the Eppendorf. The spectra of the reflectance were recorded every 2 minutes for half an hour. In Figure 4, the variations of the maximum of the first peak of the Fourier transform spectra were shown. The largest fluctuation of the peak maximum with respect to the mean value was around 2 × 10−3.
FIGURE 4
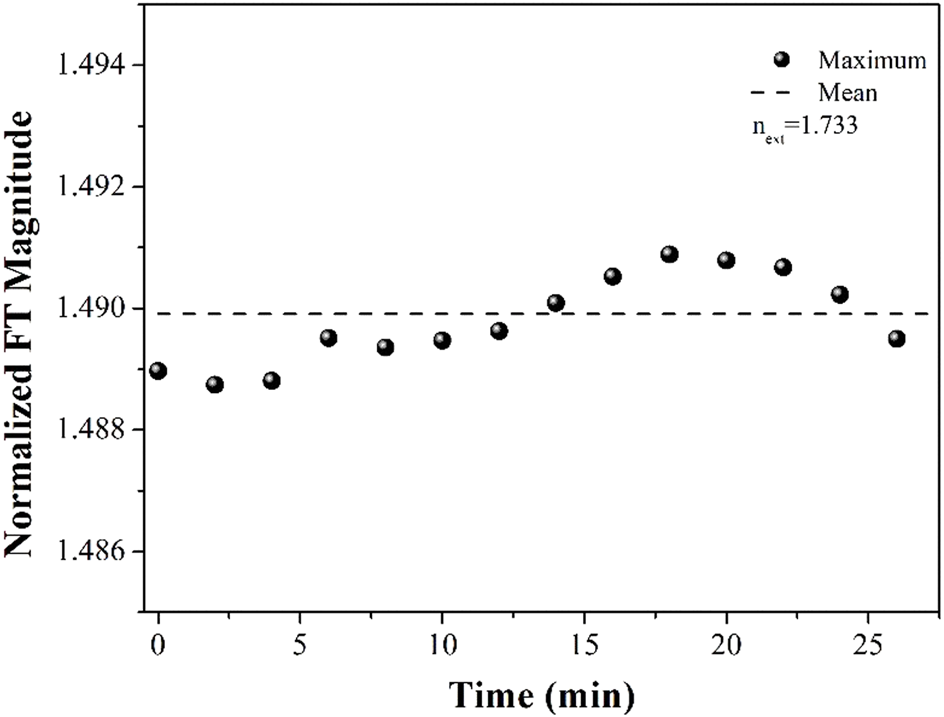
Variation of the maximum peak amplitude in time when the fiber tip was immersed in a liquid sample with a refractive index value of 1.733.
The response of the other i-HFFPI was fabricated, this one with 50.20 µm, and 37.84 µm was studied. The optical spectra of the reflectance when fiber tip was immersed in different Cargile oils are shown in Figure 5A; there is an increment in the peaks of the interference pattern as the refractive index increases. The spectra of the Fourier transform exhibit only two peaks, indicating that two of the peaks are superposed, as can be seen in Figure 5B. The amplitude of peak is almost equal to the overlapped peak when the fiber tip was surrounded by air, and the spectra were normalized to the maximal amplitude of the peak . The amplitude of the first peak increased as the refractive index of the external medium was augmented; however, for this device, the change was higher than the previous one. In this interferometer, the intensity of the beams is higher since the air cavity length is smaller. In Figure 5C, it is possible to observe that the changes in the amplitude of the overlapped peak increased when the refractive index of the external medium is augmented, where the sensitivity of this device around 0.821 RIU−1 was higher than that of the larger device as discussed previously. In this device, in which the OPL of the air and solid cavities are very similar, it was possible to measure liquids with refractive index higher than that of the SMF core. The response of this device did not show ambiguity in the refractive index range from 1 to 1.733.
FIGURE 5
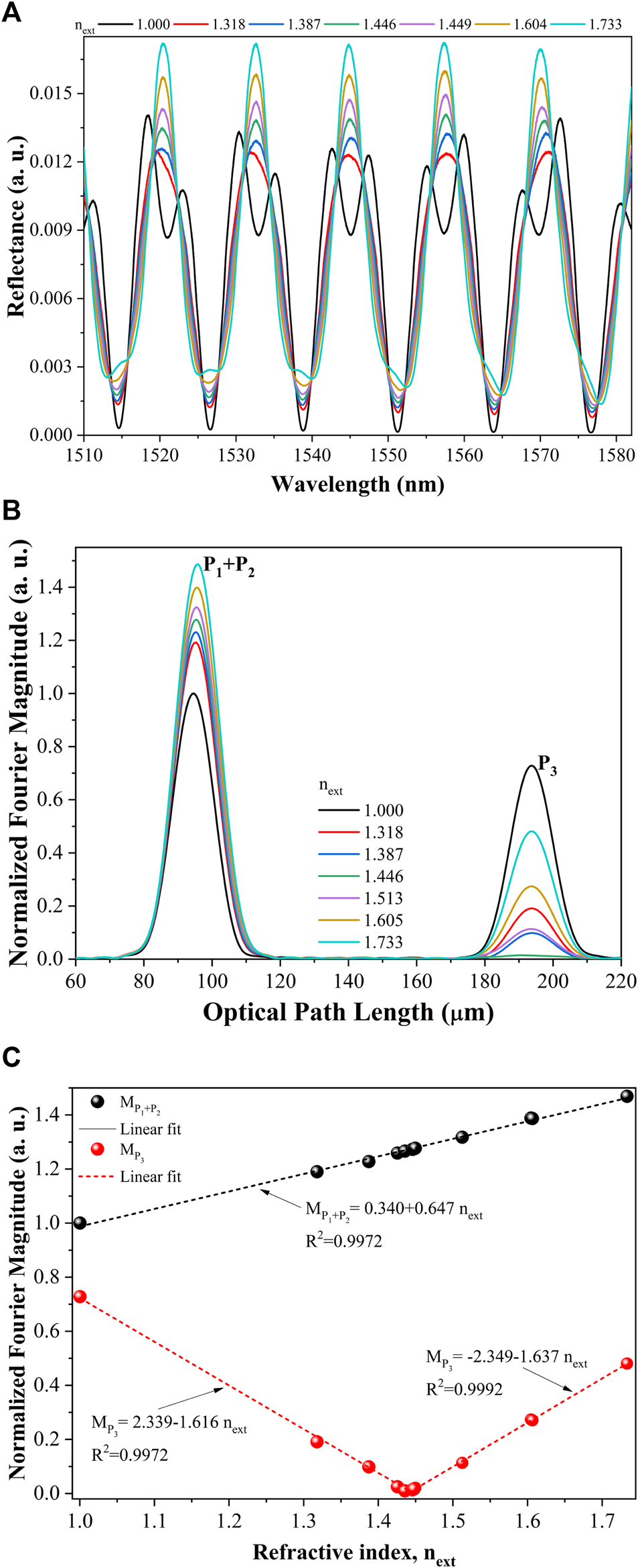
(A) Experimental spectra of the optical reflectance and (B) the corresponding Fourier transform. (C) Changes in the magnitude of the Fourier spectra peak when the i-HFFPI was immersed in different Cargille oils.
Conclusion
In summary, an optical fiber refractive index sensor with an ultra-long dynamic range [1, 1.733] was proposed and demonstrated. This sensor is based on the changes of the intensity reflected by the end-face of an isometric hybrid fiber Fabry–Perot interferometer (i-HFFPI) caused by the changes of the refractive index of the fiber tip surrounding the medium. The particular structure of the interferometer, where the optical path length of the air and solid cavities are very similar, allows correlating the refractive index of the surrounding media with the amplitude of one of the peaks of the interferometer spectra in the Fourier domain. In this i-HFFPI, it was possible to avoid the characteristic ambiguity of the FR-OFRIS without the need to coat the fiber tip end-face with a high refractive index thin film. The sensibility of the sensor can be improved by reducing the length of the two cavities of the interferometer. The interrogation technique of this FR-OFRIS is based on tracking the amplitude of one of the peaks of the Fourier spectra, which is simple to be accomplished and easy to be performed online for real-time measurement applications. The structure and fabrication process of the i-HFFPI is also simple.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
CD-F: methodology, formal analysis, investigation, writing—original draft, visualization, and software. DM-H: conceptualization, methodology, formal analysis, writing—original draft, validation, visualization, and software. AV-H: methodology and data analysis. AR: analysis of results, review, and editing. OR-Q: visualization and software. RO-V: conceptualization, writing—review and editing, and resources. All authors contributed to manuscript revision, and read and approved the submitted version.
Funding
This study was funded by Consejo Nacional de Ciencia y Tecnología (México).
Acknowledgments
The authors want to acknowledge the Consejo Nacional de Ciencia y Tecnología (Mexico) CONACYT for financial support through the Ph. D. scholarship of C. E. Domínguez-Flores and K. Reyes, and postdoctoral scholarship of O. Rodríguez Quiroz.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Aronne G. Malara P. (2019). Fiber‐optic Refractometer for In Vivo Sugar Concentration Measurements of Low‐nectar‐producing Flowers. New Phytol.224, 987–993. 10.1111/nph.16084
2
Brientin A. Leduc D. Gaillard V. Girard M. Lupi C. (2021). Numerical and Experimental Study of a Multimode Optical Fiber Sensor Based on Fresnel Reflection at the Fiber Tip for Refractive index Measurement. Opt. Laser Techn.143, 107315. 10.1016/j.optlastec.2021.107315
3
Chen P. Shu X. Cao H. Sugden K. (2017). High-sensitivity and Large-Dynamic-Range Refractive index Sensors Employing Weak Composite Fabry-Perot Cavities. Opt. Lett.42, 3145–3148. 10.1364/OL.42.003145
4
Choi H. Y. Mudhana G. Park K. S. Paek U.-C. Lee B. H. (2010). Cross-talk Free and Ultra-compact Fiber Optic Sensor for Simultaneous Measurement of Temperature and Refractive index. Opt. Express18, 141. 10.1364/OE.18.000141
5
Dominguez-Flores C. E. Rodriguez-Quiroz O. Monzon-Hernandez D. Ascorbe J. Corres J. M. Arregui F. J. (2020b). Dual-Cavity Fiber Fabry-Perot Interferometer Coated with SnO2 for Relative Humidity and Temperature Sensing. IEEE Sensors J.20, 14195–14201. 10.1109/JSEN.2020.3008167
6
Dominguez-Flores C. E. Rodriguez-Quiroz O. Monzon-Hernandez D. (2021a). Simple Signal Processing Method to Enlarge the Dynamic Range of the Fresnel Reflection-Based Fiber Fabry-Perot Refractive index Sensors. J. Lightwave Technol.39, 1497–1503. 10.1109/JLT.2020.3039419
7
Flores-Bravo J. A. Fernandez R. Antonio Lopez E. Zubia J. Schulzgen A. Amezcua Correa R. et al (2021). Simultaneous Sensing of Refractive Index and Temperature with Supermode Interference. J. Lightwave Technol.39, 7351–7357. 10.1109/JLT.2021.3113863
8
Gong Y. Yu Guo Y. Yun-Jiang Rao Y. J. Tian Zhao T. Yu Wu Y. (2010a). Fiber-Optic Fabry-Pérot Sensor Based on Periodic Focusing Effect of Graded-Index Multimode Fibers. IEEE Photon. Technol. Lett.22, 1708–1710. 10.1109/LPT.2010.2082518
9
Gong Y. Zhao T. Rao Y.-J. Wu Y. Guo Y. (2010b). A ray-transfer-matrix Model for Hybrid Fiber Fabry-Perot Sensor Based on Graded-index Multimode Fiber. Opt. Express18, 15844. 10.1364/oe.18.015844
10
Jáuregui-Vázquez D. Estudillo-Ayala J. Rojas-Laguna R. Vargas-Rodríguez E. Sierra-Hernández J. Hernández-García J. et al (2013). An All Fiber Intrinsic Fabry-Perot Interferometer Based on an Air-Microcavity. Sensors13, 6355–6364. 10.3390/s130506355
11
Jiang M. Li Q.-S. Wang J.-N. Jin Z. Sui Q. Ma Y. et al (2013a). TiO_2 Nanoparticle Thin Film-Coated Optical Fiber Fabry-Perot Sensor. Opt. Express21, 3083. 10.1364/oe.21.003083
12
Jiang M. Qiu-Shun Li Q. S. Jun-Nan Wang J. N. Wei-Guo Yao W. G. Zhongwei Jin Z. Qingmei Sui Q. et al (2013b). Optical Response of Fiber-Optic Fabry-Perot Refractive-index Tip Sensor Coated with Polyelectrolyte Multilayer Ultra-thin Films. J. Lightwave Technol.31, 2321–2326. 10.1109/JLT.2013.2262022
13
Joel G. Okoro L. N. (2019). Recent Advances in the Use of Sensors and Markers for Fuel Adulteration Detection : A Review. Int. J. Res. Sci. Innov.VI, 82–89. 10.51244/IJRSI
14
Li J. (2020). A Review: Development of Novel Fiber-Optic Platforms for Bulk and Surface Refractive index Sensing Applications. Sensors Actuators Rep.2, 100018. 10.1016/j.snr.2020.100018
15
Li Z. Liao C. Wang Y. Dong X. Liu S. Yang K. et al (2014). Ultrasensitive Refractive index Sensor Based on a Mach-Zehnder Interferometer Created in Twin-Core Fiber. Opt. Lett.39, 4982. 10.1364/ol.39.004982
16
Liu B.-H. Jiang Y.-X. Zhu X.-S. Tang X.-L. Shi Y.-W. (2013). Hollow Fiber Surface Plasmon Resonance Sensor for the Detection of Liquid with High Refractive index. Opt. Express21, 32349. 10.1364/oe.21.032349
17
Liu X. Jiang M. Sui Q. Geng X. Song F. (2017). HCPCF-based In-Line Fiber Fabry-Perot Refractometer and High Sensitivity Signal Processing Method. Photonic Sens7, 336–344. 10.1007/s13320-017-0392-6
18
Lu P. Harris J. Wang X. Lin G. Chen L. Bao X. (2012). Tapered-fiber-based Refractive index Sensor at an Air/solution Interface. Appl. Opt.51, 7368. 10.1364/ao.51.007368
19
Meng H. Shen W. Zhang G. Wu X. Wang W. Tan C. et al (2011). Michelson Interferometer-Based Fiber-Optic Sensing of Liquid Refractive index. Sensors Actuators B: Chem.160, 720–723. 10.1016/j.snb.2011.08.054
20
Meyer M. S. Eesley G. L. (1987). Optical Fiber Refractometer. Rev. Scientific Instr.58, 2047–2048. 10.1063/1.1139513
21
Ran Z. L. Rao Y. J. Liu W. J. Liao X. Chiang K. S. (2008). Laser-micromachined Fabry-Perot Optical Fiber Tip Sensor for High-Resolution Temperature-independent Measurement of Refractive index. Opt. Express16, 2252. 10.1364/oe.16.002252
22
Rodríguez-Quiroz O. Domínguez-Flores C. E. Monzón-Hernández D. Morales-Narváez E. Minkovich V. P. López-Cortés D. (2020). Unambiguous Refractive-index Measurement in a Wide Dynamic-Range Using a Hybrid Fiber Fabry-Perot Interferometer Assisted by a Fiber Bragg Grating. Opt. Laser Techn.128, 106236. 10.1016/j.optlastec.2020.106236
23
Rodriguez-Quiroz O. Dominguez-Flores C. E. Monzon-Hernandez D. Moreno-Hernandez C. (2019). Hybrid Fiber Fabry-Perot Interferometer with Improved Refractometric Response. J. Lightwave Technol.37, 4268–4274. 10.1109/JLT.2019.2922836
24
Urrutia A. Del Villar I. Zubiate P. Zamarreño C. R. (2019). A Comprehensive Review of Optical Fiber Refractometers: Toward a Standard Comparative Criterion. Laser Photon. Rev.13, 1900094. 10.1002/lpor.201900094
25
Wang T. Wang M. (2012). Fabry-Pérot Fiber Sensor for Simultaneous Measurement of Refractive Index and Temperature Based on an In-Fiber Ellipsoidal Cavity. IEEE Photon. Technol. Lett.24, 1733–1736. 10.1109/LPT.2012.2212184
26
Zhang W. Li H. Zhu L. Dong M. Meng F. (2021). Dual-Parameter Optical Fiber Probe Based on a Three-Beam Fabry-Perot Interferometer. IEEE Sensors J.21, 4635–4643. 10.1109/JSEN.2020.3034915
27
Zhang Z. He J. Du B. Zhang F. Guo K. Wang Y. (2018). Measurement of High Pressure and High Temperature Using a Dual-Cavity Fabry-Perot Interferometer Created in cascade Hollow-Core Fibers. Opt. Lett.43, 6009–6012. 10.1364/OL.43.006009
28
Zhou K. Yan Z. Zhang L. Bennion I. (2011). Refractometer Based on Fiber Bragg Grating Fabry-Pérot Cavity Embedded with a Narrow Microchannel. Opt. Express19, 11769–11779. 10.1364/oe.19.011769
29
Zhu C. Huang J. (2021). Microwave-photonic Optical Fiber Interferometers for Refractive index Sensing with High Sensitivity and a Tunable Dynamic Range. Opt. Lett.46, 2180. 10.1364/ol.420618
Summary
Keywords
refractometer, optical sensor, fiber optics, Fabry–Perot interferometer, Fourier analysis
Citation
Domínguez-Flores CE, Valdés-Hernández AI, Reyes AK, Monzón-Hernández D, Rodríguez-Quiroz O and Ochoa-Valiente R (2022) Ultra-Long Range Refractive Index Fiber Sensor. Front. Sens. 3:855251. doi: 10.3389/fsens.2022.855251
Received
14 January 2022
Accepted
03 March 2022
Published
05 April 2022
Volume
3 - 2022
Edited by
Bing Sun, Nanjing University of Posts and Telecommunications, China
Reviewed by
Jin Li, Northeastern University, China
Xinghu Fu, Yanshan University, China
Xizhen Xu, Shenzhen University, China
Updates
Copyright
© 2022 Domínguez-Flores, Valdés-Hernández, Reyes, Monzón-Hernández, Rodríguez-Quiroz and Ochoa-Valiente.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Monzón-Hernández, dmonzon@cio.mx
This article was submitted to Physical Sensors, a section of the journal Frontiers in Sensors
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.